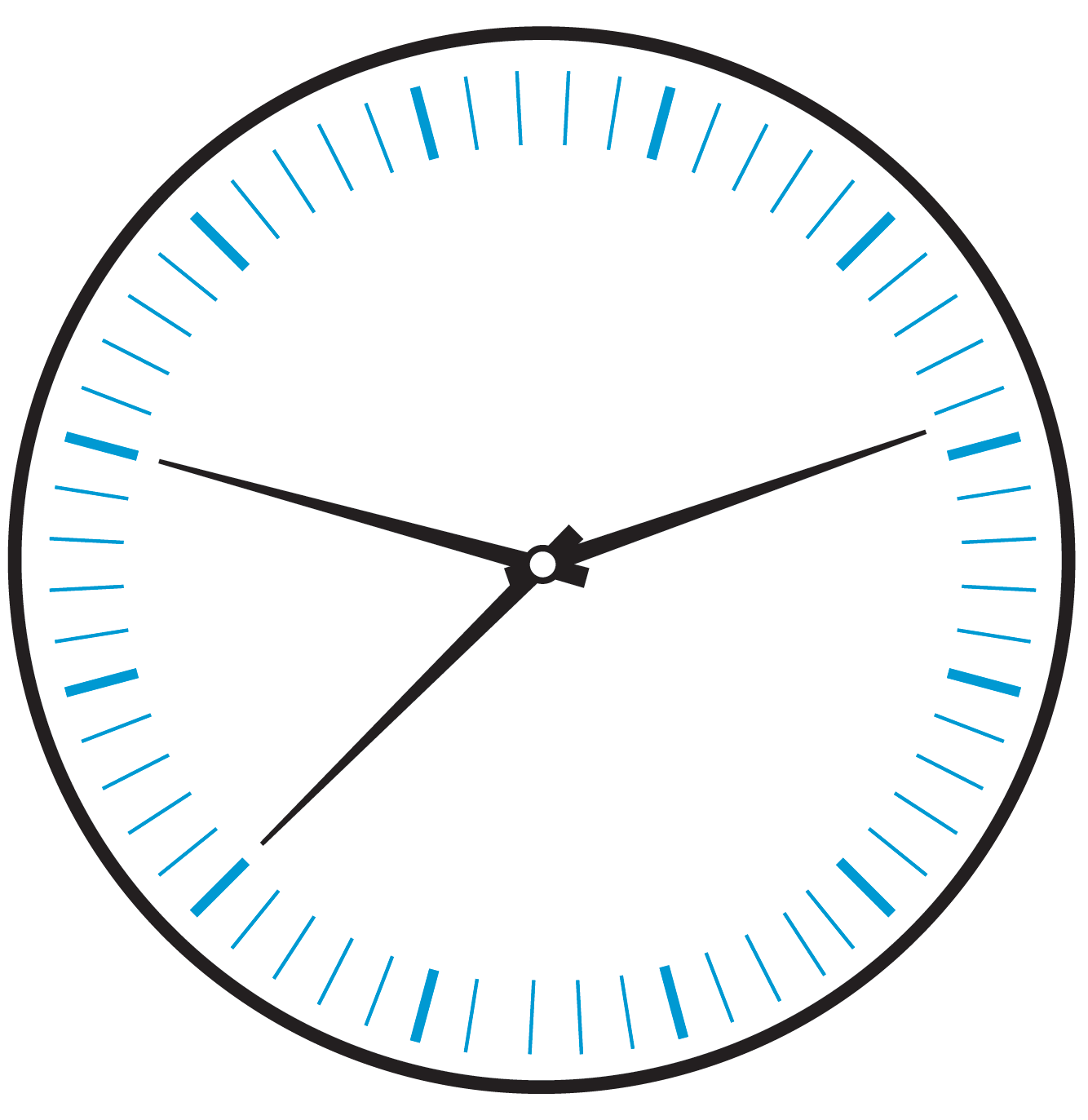
"Hands A and C are pointing exactly at hour marks. If one of these two hands is the hour hand, the minute and second hands should both be on top of each other and point at 12. Because this is not the case, B must be the hour hand. Because the minute hand points to a full minute, the second hand must point to 12."
"In the first possibility, A is the second hand, and C is the minute hand. Then A is on 12, and C is on 2, and it is 10 minutes past the hour. In that scenario, the hour hand must have traveled 1060 = 16 of the way from one hour mark to the next. But the picture shows that it has already covered more than 45 of the distance, so this possibility is ruled out."
Three identical-length hands move smoothly on a dial with hour and minute markers but no numbers, so the 12 marker is ambiguous. Two hands on the left (A lower, C higher) sit exactly on hour markers while the right hand B lies between an hour and a minute marker. If either left hand were the hour hand, the other two hands would coincide at 12, which they do not; therefore B is the hour hand. The minute hand must point to a full minute, forcing the second hand to point to 12. Comparing possibilities yields A as minute and C as second, giving exactly 4:50:00.
Read at www.scientificamerican.com
Unable to calculate read time
Collection
[
|
...
]