Surface optimization governs the local design of physical networks - Nature

"The vascular system and the brain are examples of physical networks that differ from the networks typically studied in network science owing to the tangible nature of their nodes and links, which are made of material resources and constrain their layout. The importance of these material factors has been noted in many disciplines: as early as 1899, Ramón y Cajal suggested that we must consider the laws conserving the 'wire' volume to explain neuronal design8"

"Today, wiring optimization is used to account for the morphology and the layout of a wide range of physical systems10,11, from the distributions of neuronal branch sizes12 and lengths13 to the morphology of plants14, the structure15 and flow16 in transport networks, the layout of supply networks17, the wiring of the Internet18 or the shape of inter-nest trails built by Argentine ants19 and the design of 3D-printed tissues with functional vasculature20."

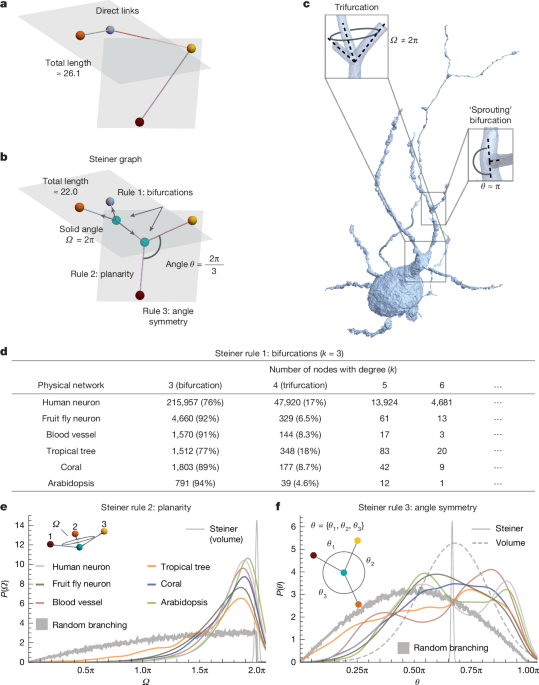
Physical networks such as vascular systems and brains differ from abstract networks because their nodes and links are material and impose spatial constraints. Historical work invoked volume conservation and volume minimization, leading to concepts such as conserving 'wire' volume and Murray's law for vascular branching. The optimal wiring hypothesis models physical networks as connected one-dimensional wires minimizing total length, with Steiner graphs predicting optimal layouts. Limited high-quality structural data previously constrained empirical tests to single neuron branches and ant tunnels, producing mixed evidence. Recent advances in microscopy and three-dimensional reconstruction now provide detailed 3D structures across systems, enabling systematic evaluation of wiring optimization predictions.

Read at Nature